0、关于
Q-learning与DQN
通过当前observation与下一步obs_获得两个预测值V来选择Action,当然这个缺点很明显:可视野很小。
Policy Gradients
通过不断地对每一回合各参数的的决策记录来进行复盘学习,当然这样效果是显而易见的,运算速度相对来说会变得慢。
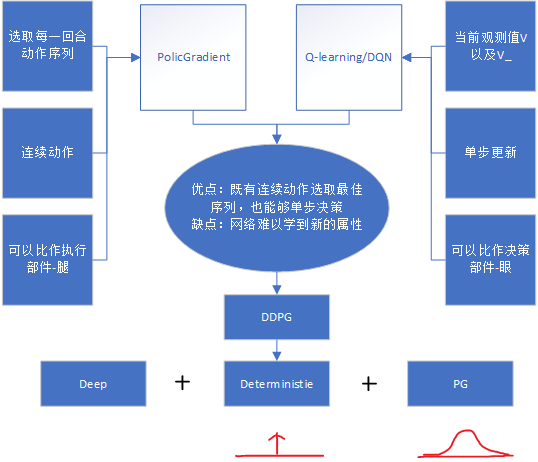
所以呢,两种方式结合一下得到类似于Actor-Critic的网络结构,把actor作为执行机构,critic作为判断机构能够给予执行机构指引,一个似眼,一个像腿。
1、DQN
QLearning是reninforcement learning中value-based的方法。Q即为Q(s,a),是在某一时刻的 state 下(s∈S),采取 动作action (a∈A)获得收益的期望,环境会根据agent的动作反馈相应的回报reward,所以算法的主要思想就是将State与Action构建成一张Q-table来存储Q值,然后根据Q值来选取能够获得最大的收益的动作,也就是贪婪的方法。
可描述如下:
1
2
3
4
5
6
7
1、初始化状态 s,alpha,gamma,Q空表
2、进入 episode 循环
3、基于状态s-->根据Q或者随机选择一个动作 a
4、执行动作a, 从环境获得 奖励r和下一个状态 s_
5、更新Q值: Q(s,a)= Q(s,a)+alpha*loss , loss=R+gamma*maxQ(s_,A)-Q(s,a) # a是预估值
6、s = s_
7、若 episode 未结束,回到 2
2、Policy Gradients
什么是策略?
1、对于回合制任务,可以定义性能的度量为一回合中能够取得的总收益 J(theta) = E * sum(0-T)(Rk)
2、对于回合制任务,也可以在回合制任务里面引入衰减率gamma,来更多地强调近期的收益 J(theta) = E * sum(0-T)(gamma^(k-1)Rk)
3、对于连续任务,由于任务不会终结,那么总收益常常会发散,这时就必须加入衰减率,来保证其收敛,这样可以得到相应的性能度量 J(theta) = E * sum(0-inf)(gamma^(k-1)Rk)
而这里使用的策略梯度决策(PG)是一种不通过分析每一步动作a所得到的回报r来的策略,简单来说,在走迷宫的游戏中,PG对一局游戏的连续区间所执行的动作a进行学习,类似于复盘学到哪一个位置怎么走是最有益的。这样的方法能够防止value based算法在感受野很小的地方来回往复选择,在无关痛痒的地区浪费更多的时间犹豫不定,依靠低概率的随机选择走出新的一步。
PG通过观测信息(之前游戏中此位置所执行过的动作)选出一个action直接进行反向传播,当然出人意料的是他并没有误差,而是利用动作reward直接对选择行为的可能性进行增强和减弱,好的行为会被增加下一次被选中的概率,不好的行为会被减弱下次被选中的概率。
几个注意点:
1
2
3
算法输出的是动作的概率,而不是Q值。
损失函数的形式为:loss= -log(prob)*Vt
需要一次完整的episode才可以进行参数的更新
介绍完上面两种方法后相互之间优势互补能有更好的效果,下面图也可以说明然后该怎么做:
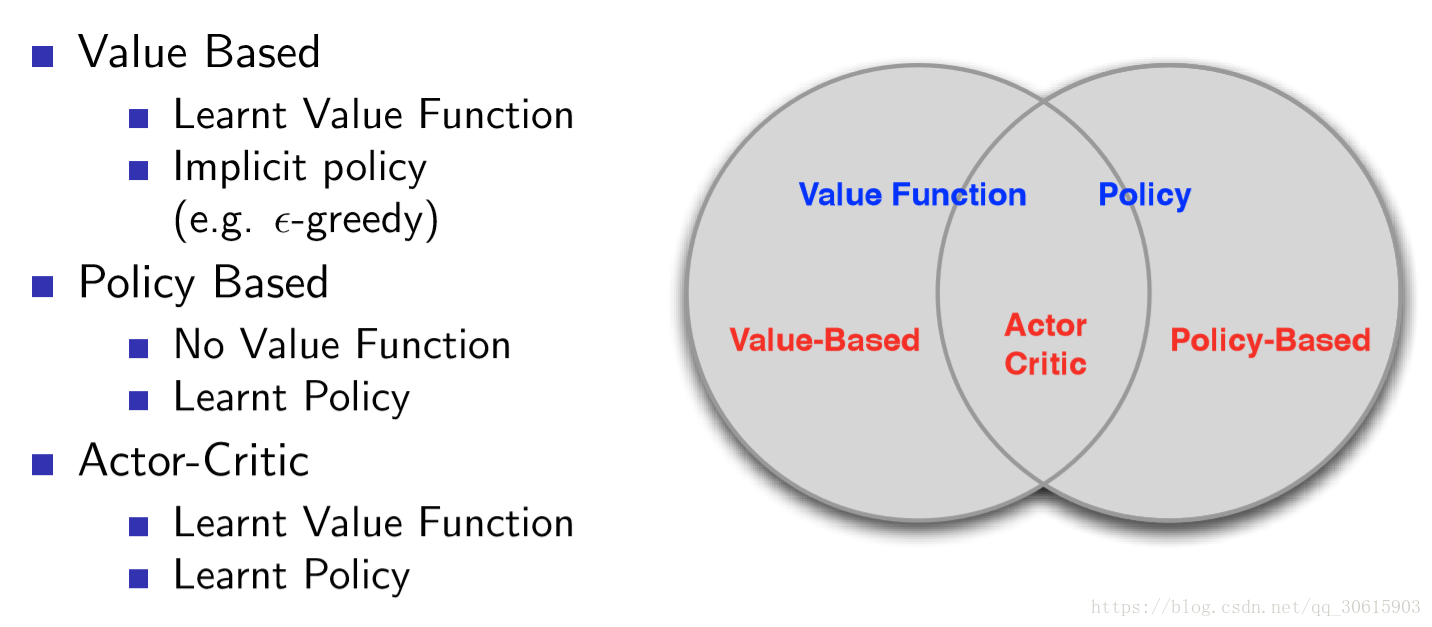
3、Actor-Critic
基于值的强化学习算法的基本思想是根据当前的状态s,计算采取每个动作a的价值r,然后根据价值贪心的选择动作或者一定概率随机选择动作。Policy Gradient中奖惩信息是通过走完一个完整的episode来计算得到的,r的计算也是综合考虑了整个回合的加权回报。这导致了整个网络的学习速率很慢,需要很长时间才可以学到东西。Actor不断迭代,得到每一个状态s下选择每一动作a的合理概率,Critic也通过迭代不断完善每个状态s下选择每一个动作a的奖惩值r。
- Actor-loss还是使用的Policy Gradient中提到过的loss= -log(prob)*vt,只不过这里的vt换成了由Critic网络计算出的时间差分误差td_error,反向传播回网络中,
tf.train.AdamOptimizer(lr).minimize(-self.exp_v)这一句不仅可以计算出梯度同时还进行了优化。
不过问题肯定还是会有的:
- Actor-Critic 涉及到了两个神经网络,每个net各有2层layer 能够在执行完每一个动作之后更新参数, 但是参数前后都存在相关性, 导致神经网络只能片面的看待问题, 甚至学不到东西。
相关注意点:
1
2
3
4
5
6
7
8
9
# Actor
1、算法输出的是动作的概率,而不是Q值。
2、损失函数的形式为:loss= -log(prob)*Td_error # 这里的Vt 换成了Td_error
3、需要一次完整的episode才可以进行参数的更新
# Critic
1、初始化状态 alpha,gamma,Q空表,从Actor获得S,s,A,a等
2、基于状态s,从Actor_net 获得真实动作A 预估动作a_
3、更新Q值: target_q= R+gamma*q , 损失也使用平方差:loss=(R+gamma*maxQ(S,A)-Q(s,a))^2 # a是预估动作 损失也换用了平方差函数
用流程图大致描述一下:
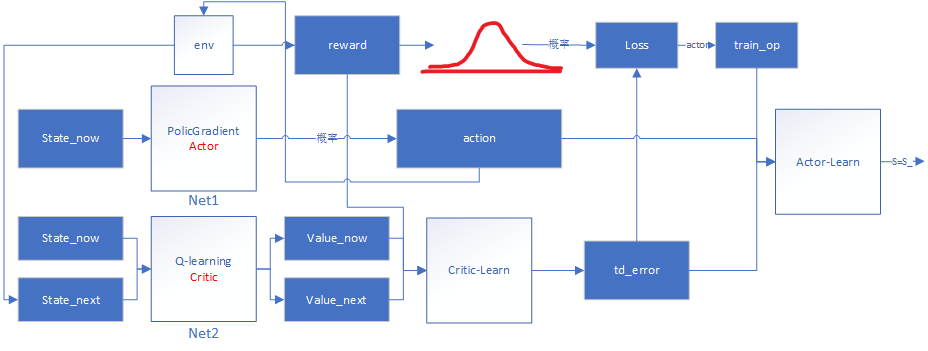
4、DDPG
Actor-Critic + DQN = DDPG Q-learning + Deep = DQN
还要再核对一下tensorboard流程图
loading……

5、蒙特卡洛梯度策略强化算法

ps: markdown公式:{s_1,a_1,r_1, \dots, s_(T-1),a_(T-1),r_T}\sim\pi\theta
1
2
先随机初始化策略函数的参数θ,对当前策略下的一个Episode
从t=1到t=T-1间的每一个时刻,计算个体获得的收获 Vt,更新参数θ。如此重复每一个Episode,直到结束。
存在问题:使用蒙特卡洛策略梯度算法收敛速度慢,需要的迭代次数长,还存在较高的变异性。
Github-Pytorch例程推荐
参考
Q-learning详解
PG-theorem推导
蒙特卡洛梯度策略强化算法
关于公式的介绍-比较详细×推荐