0、关于
公式推导最大后验推导和贝叶斯推导之间选一个.
WSY之前问我当初卡尔曼C语言的实现问题,翻了翻书顺便对比了下代码,这里总结一下.
1、参考 <概率机器人> 书中的 Algorithm-Kalman_filter
(1)准备工作
先验预测值 x'
后验测量值 z
(1.1)x’(k) 状态预测公式
1
2
3
Predict part:
x'(k) = Ax(k-1) + Bu(k-1) + w(k-1)
预测 上一时刻估计 控制 系统误差
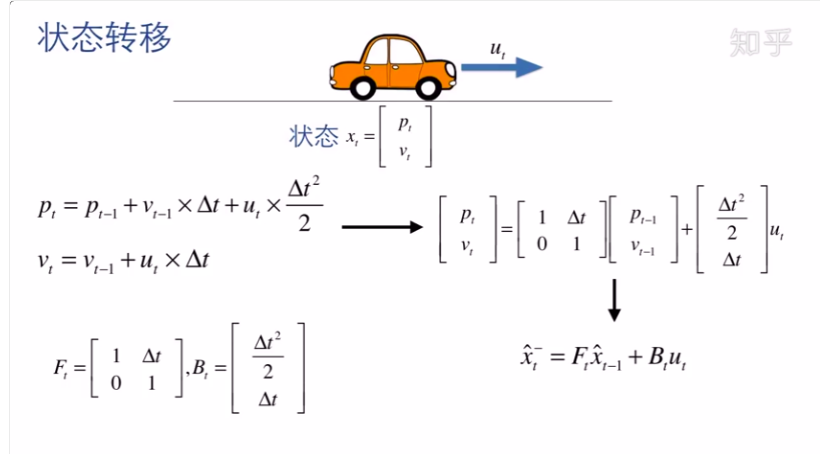
以具体的匀加速运动的实例来说:
x(k-1)这个2*1维矩阵为上一时刻 位移与速度 两个状态变量的估计值
u(k-1)是上一时刻系统输入量,这里是作用的 合外力
w(k-1)为系统噪声,可设置常量
A,B为描述匀加速状态的公式矩阵,位移公式与速度公式转化而来
上式即为我们根据k-1时刻状态由公式预测得到k时刻的结果.我们都会想:速度能计算出，位移也能计算出,只要知道初始时刻的状态然后不断迭代不就能够得到当前时刻的状态(先验)了吗?当然这是在能够推导出数学模型以及迭代不出错的前提下,如果出错后小误差也会被放大,从而影响整个结果的准确性,所以后面还需要反馈的测量值(后验)进行修正.
(1.2)z(k) 状态测量真实值传感器采集
表达式:z(k) = Hx(k) + v(k),作为实参传入.
1
2
3
4
measurement predict:
z'(k) = Hx'(k)
测量值预测 预测
Ｈ＝［１ ０］
真实状态的测量值z(k)是通过观测矩阵H通过将状态空间中变量转换到观测空间,v为测量过程中存在的高斯噪声,这一过程都在函数外进行,作为已知参数传入函数进行计算.
拿匀加速例子来说,这里的测量量z即由传感器测量得到的位移值.
通过计算测量值预测值z’,可以计算出与实际值z之间的偏差,用来修正最终估计值.
(2)x(k) 使用KF计算估计值
1
2
3
x(k) = x'(k) + K(z(k)-z'(k))
当前状态估计值 预测 + 增益(测量值-测量预测值)
return x(k) 残差
使用(1)得到的x’(k) ,z’(k)以及测量的z(k)在卡尔曼增益下可以计算得到当前状态的
估计值x(k),这就是我们需要的最终结果.
接下来便是怎样计算K增益.
(3)P’(k) 先验误差协方差
1
2
3
Predict part:
P'(k) = A*P(k-1)AT + Q(k)
先验 A矩阵 k-1时刻误差协方差矩阵
与(1)中求取先验x’(k)相同,这里首先求先验P’(k)矩阵.
矩阵P用来描述我们对当前预估状态信任程度,在每一轮迭代中keyP(k)数值越小,那么最终计算出的估计值x(k)可信度越高,即K值越小,反馈所起到的作用越小
(4)K 卡尔曼增益
1
2
3
H矩阵转置
K(k) = P'(K)HT / (HP'(K)HT + R)
先验均方差 测量噪声协方差
H与R往往都是常值,增益K主要看的是
先验P'(k)本身大小在噪声干扰R下所占比重,K值越小,误差协方差P(k)越小,估计值x(k)准确率越高.
(5)P(k) 误差均方差更新
1
2
P(K) = (I - K(k)H)P'(k)
单位阵 预测均方差
更新误差均方差
(n)总结
简单来说就是通过一定的动力学公式计算获得先验状态预测值(1.1),同时预测当前系统误差协方差的大小(3),通过结合误差协方差和测量误差R等计算出卡尔曼增益K(4)修饰测量值Z的可信程度,这样修正过后的先验状态x(k)即具有较高置信度(2).
卡尔曼滤波器是用于从间接和不确定测量估计系统状态的最佳估计算法.卡尔曼滤波器仅针对线性系统定义。如果有非线性系统并且想要估计系统状态，则需要使用非线性状态估计器EKF。
书中31页首先列出了线性高斯状态转移和对测量值的KF算法,公式中参数很多,在日常线性问题使 A B C I 四个参数默认取1即可.有关基础知识看一下知乎傻瓜也能看懂的卡尔曼或者简书卡尔曼C代码实现
2、思考
之前调车的时候常常会说注意看滤波后曲线对滤波前曲线的跟随性和准确性,仔细思考一下,这里所说的跟随性该怎么认为呢?
- 卡尔曼可是由计算速度快并且效果优良著称的好算法,按照我之前的理解就是
传感器采集数据Z(t)发生突变的时候滤波后结果∑(t)与μ(t)应该紧跟着发生变化,而滤除部分则是数值变化尖锐点.由此看来如果公式用的对,在一般线性问题计算过程中,滤波后数值的跟随性在响应速度上不会存在问题,跟随哪一个对象一起发生变化则是重点,所以跟随是指是否是跟对了我们想要滤波的数值对象,当然这个变量传对了就没啥问题.
那么准确性又怎么说?如果我想滤传感器传回来的采集值,是不是最后结果显示滤波后与滤波前所画出来的曲线近似完全重合才是最理想的?
- 卡尔曼算法中提到的
Q-过程误差、R-测量误差作为实际情况中很关键部分,使得真实值既不等于测量值,也不会等于预测值.课本中给出的例证也说明了这一点.
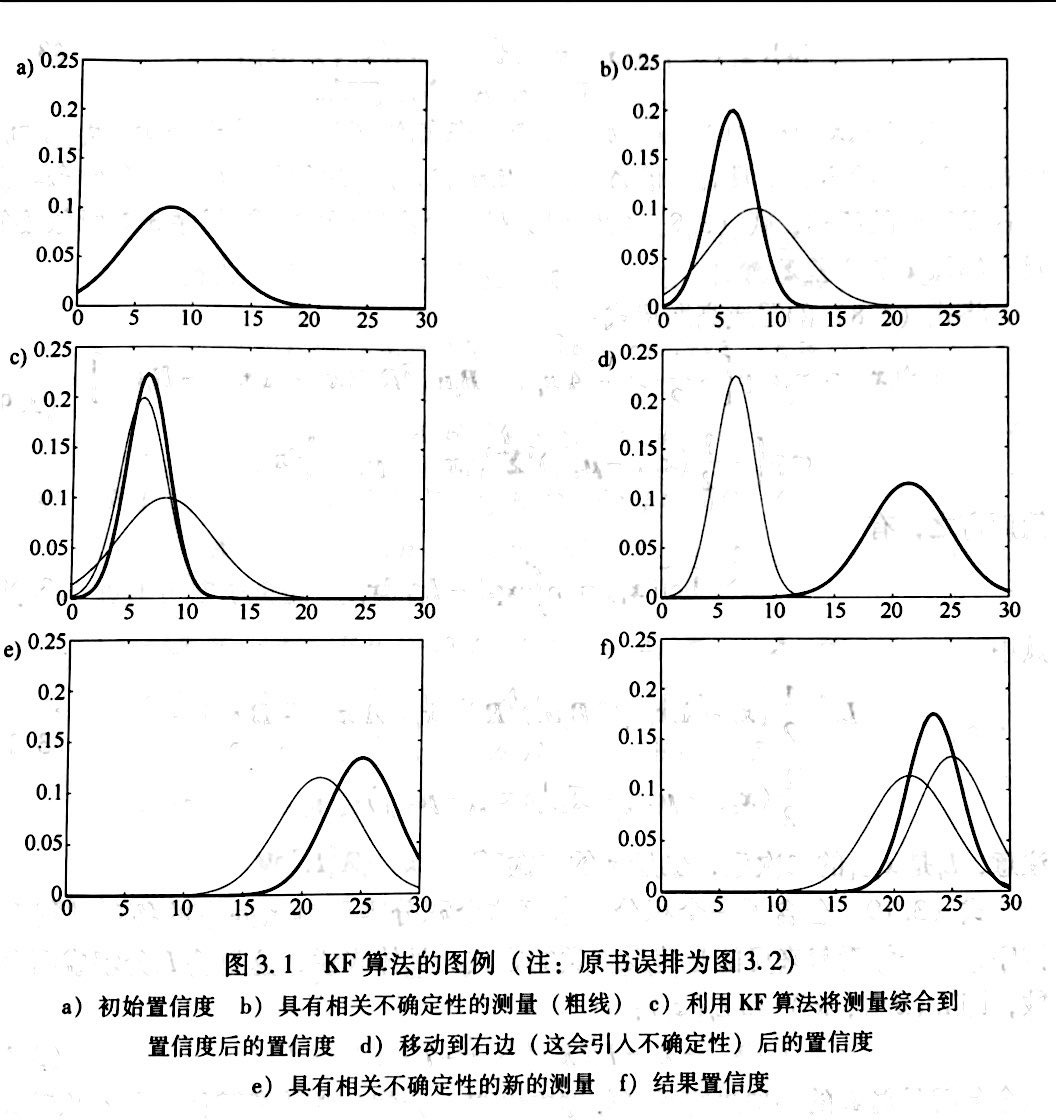
卡尔曼增益怎么起作用?
- Kt分子越大,先验预测的
方差越大,那么说明先验值准确定很低,置信度则不高.那么计算求解最优估计值的时候加大测量值Zt置信度.
概率机器人学是摒弃了可能出现的情况的单一的”最好预测”,转而使用概率的算法来表示
模糊性和置信度.
我深以为然.
3、C语言简单实现
下面是伴随十二十三十四届直立车走过的简单一阶卡尔曼函数实现,也见证了两个国一的诞生.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
float Kalman_Filter(float AccZ_Angle,float Gyropitch)
{
static float x=0; //最优角度初值
static float p=0.000001; //最优角度对应协方差初值
static float Q=0.000001; //过程噪声
static float R=0.35; //测量噪声
static float k=0; //kalman 系数
x = x + Gyropitch*0.00348f;
p = p + Q;
k = p / (p+R);
x = x + k*(AccZ_Angle-x);
p = (1-k)*p;
return x;
}
通过对姿态传感器读进来的角加速度以及角速度进行计算,并进行卡尔曼滤波后得到的概率预测角度x.
说实话,封装好的卡尔曼确实挺好用.至于卡尔曼滤波后的效果以及卡尔曼参数调整后效果我会找个直立小车进行测试,用蓝牙传输回数据再用matlab搞出曲线对比一下.
4、实验部分
卡尔曼与互补滤波的对决
小车直立控制都是通过对角加速度和角速度进行融合后得到滤波后角度进行控制,效果见下图:
- 互补滤波
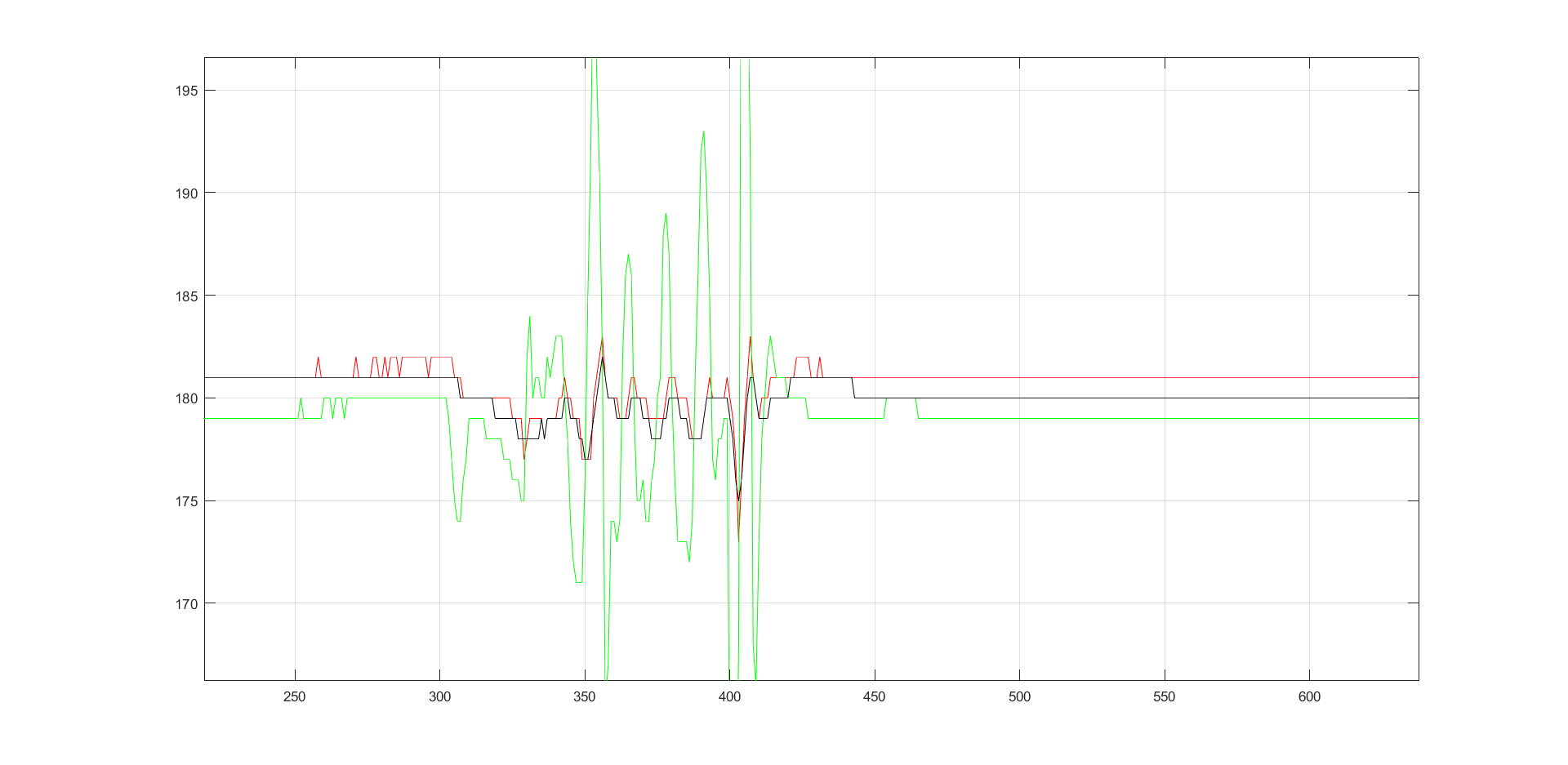
- 卡尔曼
建议先看一下线性卡尔曼公式以及滤波效果
小车姿态平稳变化效果:
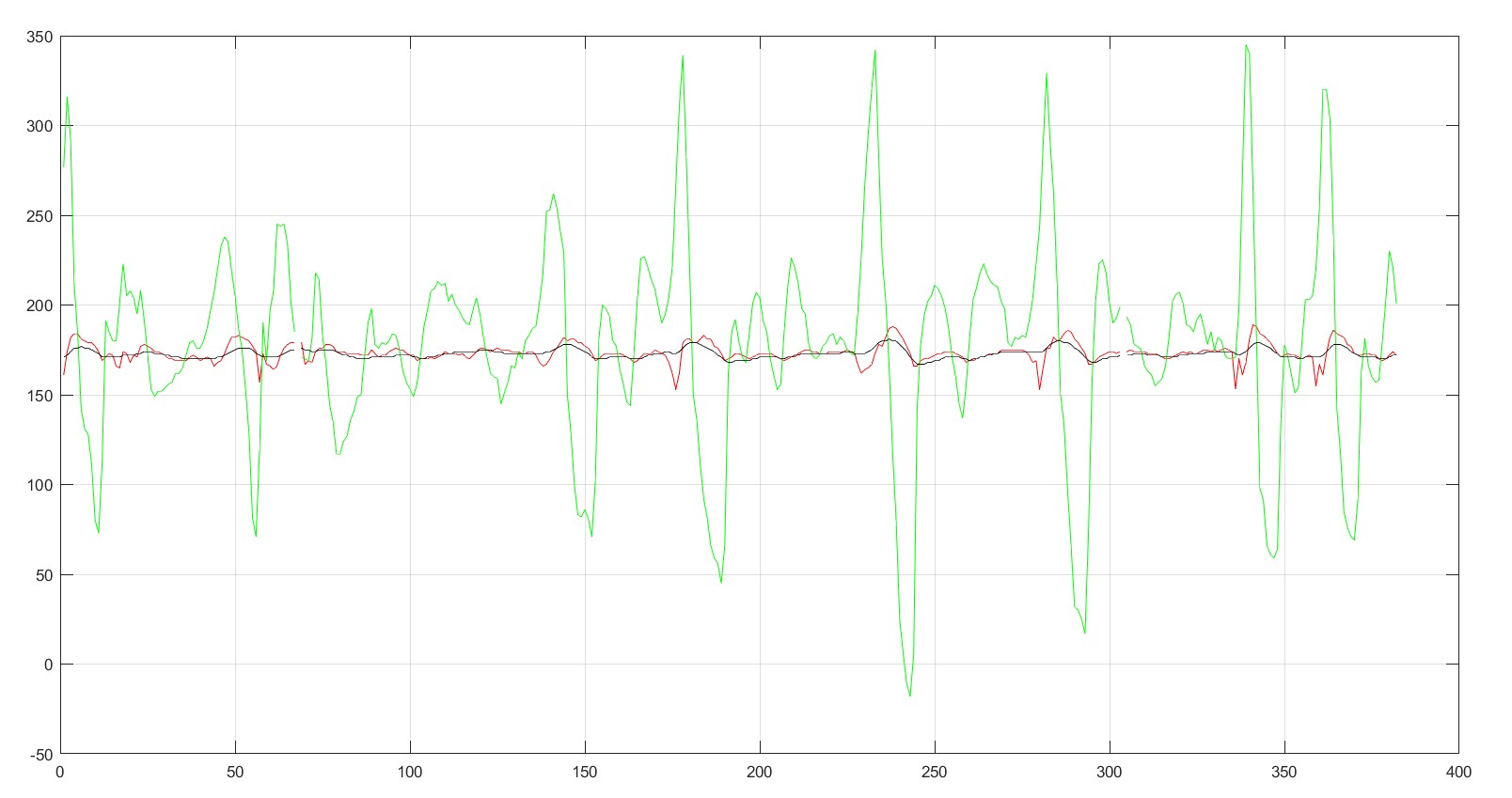外力频繁干预小车使姿态变化:
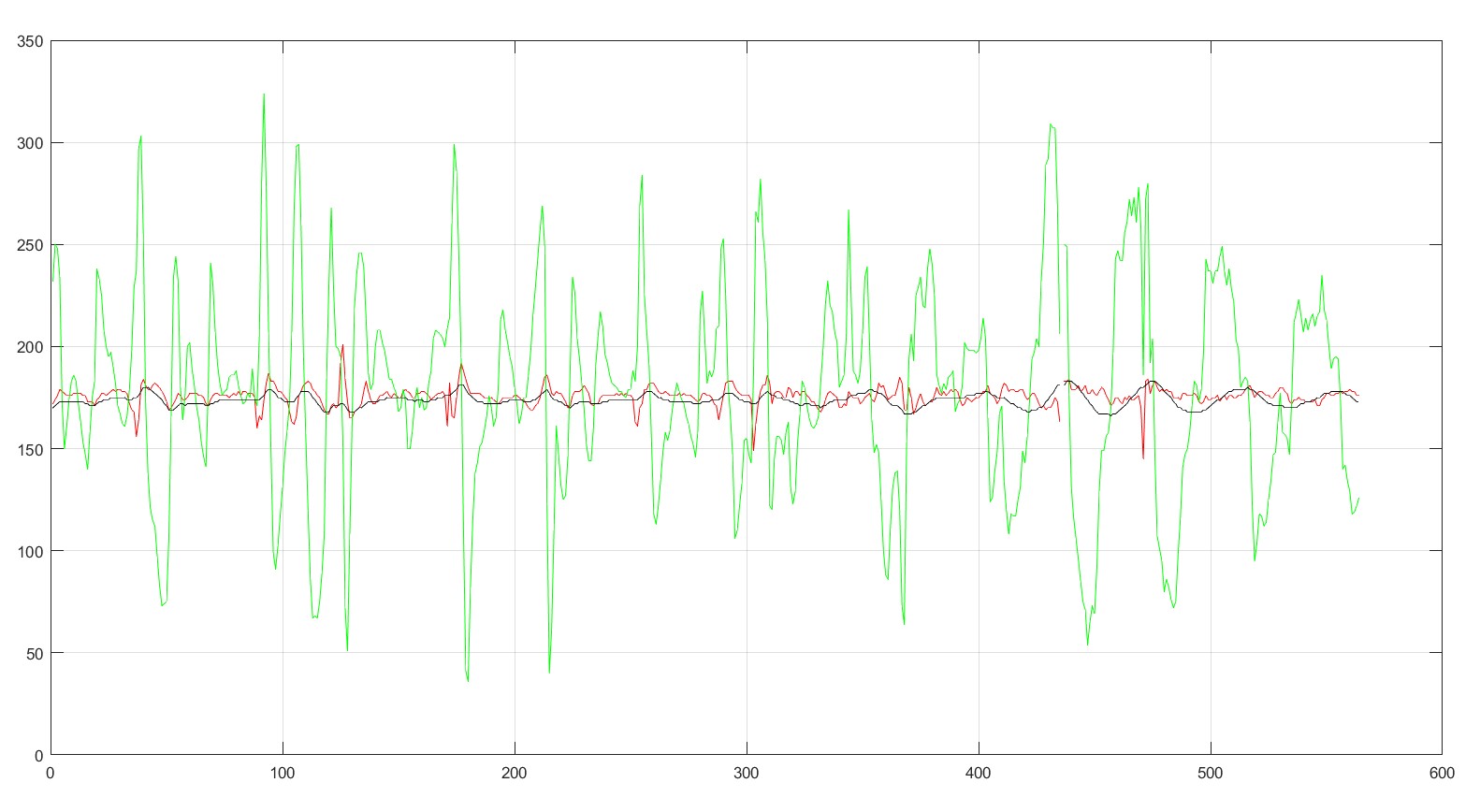
直接移植到某淘宝库上简单调试一下改改直立零点设置即可.
扩展卡尔曼EKF(One way to handle the non-linearities)
扩展卡尔曼滤波器(EKF)放宽了卡尔曼的线性化假设,这里的假设状态转移概率和测量概率由非线性函数g,h控制[书中3.2(b)].可以看出左上角的高斯分布出现了多个波峰,右上角函数也不再是线性.书中后面还给出了几种高斯分布情况下的泰勒近似,通过局部线性化可以有效的解决机器人中的非线性问题.
扩展卡尔曼高斯分布的不确定性由非线性函数变换前的高斯分布决定,高斯分布不确定性越高(概率密度越分散),EKF的随机变量密度扭曲越大